How many times have you seen the phrase: “Your password is securely encrypted”? More often than not, taking it at face value has little sense. Encryption means the data (such as the password) can be decrypted if you have the right key. Most passwords, however, cannot be decrypted since they weren’t encrypted in the first place. Instead, one might be able to recover them by running a lengthy attack. Let’s talk about the differences between encryption and hashing and discuss why some passwords are so much tougher to break.

Encryption and Hashing

Passwords are used to protect access to documents, databases, compressed archives, online accounts, and many other things one can think of. With few exceptions (such as the passwords stored in Web browsers, keychain, or IMAP/POP3 accounts), passwords are almost never stored, encrypted or not. Instead, passwords are “hashed”, or transformed with a one-way function. The result of the transformation, if one is performed correctly, cannot be reversed, and the original password cannot be “decrypted” from the result of a hash function. If you are interested in how password hashing works, check out this article: Hashing Passwords: One-Way Road to Security.

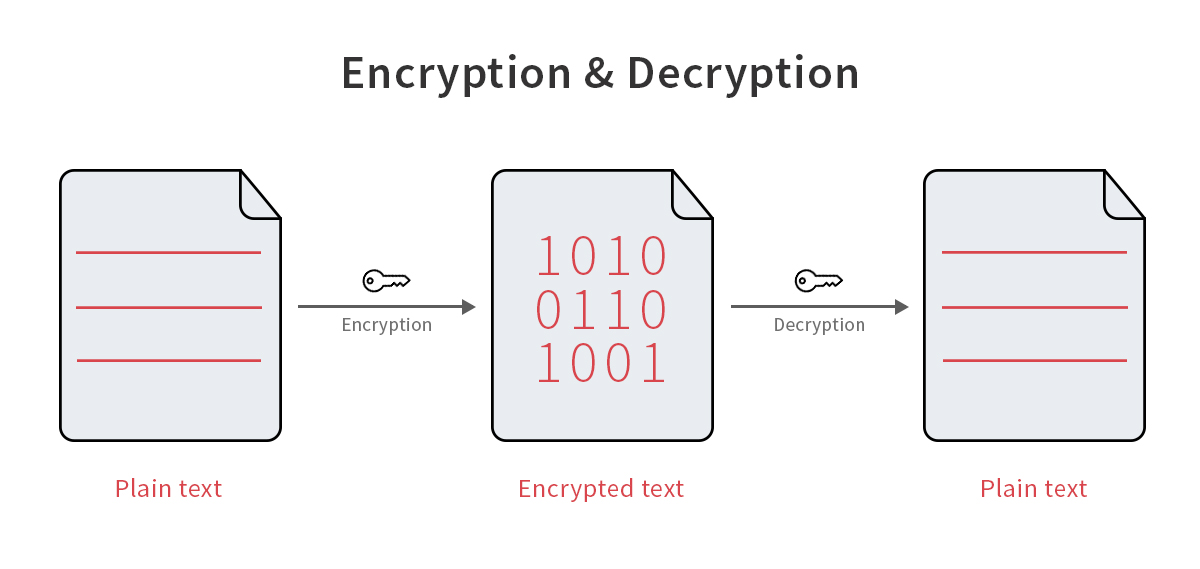
Figure 1: Encryption is a lossless, reversible, two-way transformation

What’s hashing all about? Hashing is a deliberately one-way algorithm that transforms data of any size to a string of a fixed size.

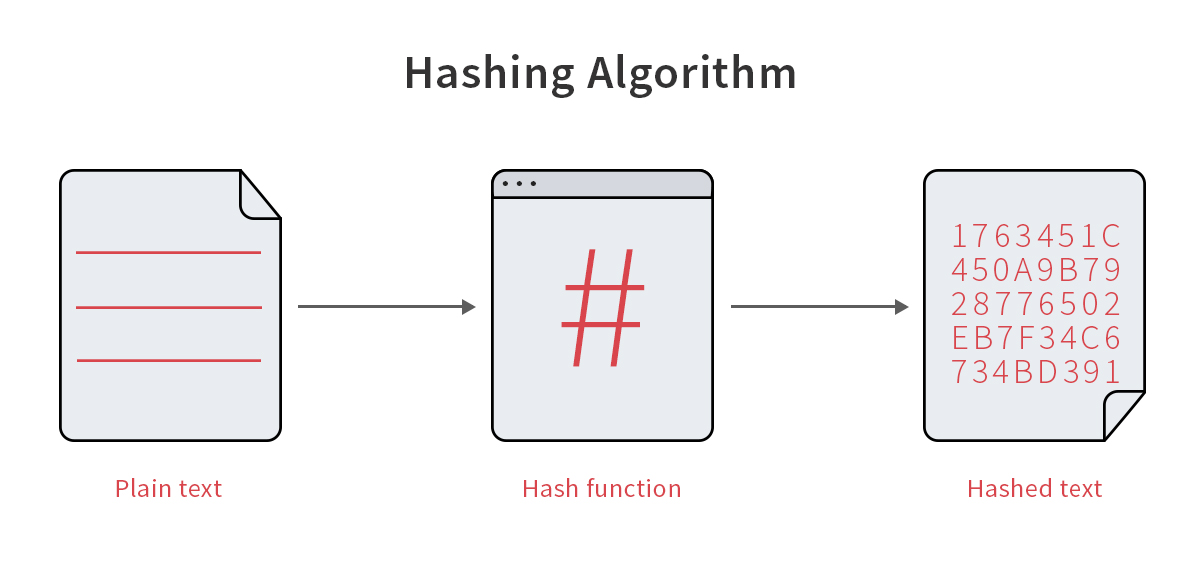
Figure 2: Hashing is a lossy, irreversible, one-way transformation

Cryptographic hash algorithms have several interesting properties. There must be no collisions. Flipping just one single bit in the original data set produces a completely new hash that does not even resemble the original. Have a look at these two hashes:

Original text: 000000000000
SHA-1: C2311E92660DE47B456E721B0DABC9F857AB48F0

Original text: 000000000001
SHA-1: F6A8135A89118200A9CC55D456C4D9A2D319FA29

As you can see, there is literally nothing in common between the two hash strings. You can play with hash values by using the simple online SHA-1 hash generator.

While the good hashing algorithms ensure that the checksum changes dramatically even with the flip of single bit, not everyone uses good hash functions. In a recent publication Tally ERP 9 Vault: How to Not Implement Password Protection I wrote about a hash function that was quite amusing. The developers of Tally Vault decided to give existing hash functions a pass, implementing their very own hash algorithm. They did an amazingly bad job in designing a hash function that only demonstrated slight modifications of the hash value with similarly slight alteration of the user’s password. This suggests a horribly weak implementation of key derivation in Tally Vault, making it an easy target for brute-force attack (which was confirmed later on). Considering that numerous cryptographically strong hash functions exist for a very long time, this result is truly amazing (as in “amazingly bad”).

Hashing must be implemented properly to provide secure password protection.

Today, we frequently use hash functions such as SHA-256 and SHA-512. The older SHA-1 is being slowly phased out after the purely theoretic discovery of the first collision back in 2017 made collision attacks practical.

Source: Google security blog

The choice of a hashing algorithm is crucial for password security.

More exotic hash functions such as Whirlpool also exist. Regardless of the name, hash functions must be quick to calculate, making it easy to both create and verify hashes. At the same time, it must be impossible to re-create the original data based on its hash function.

Impossible? Yes, when it comes to hashing large sets of data (e.g. the entire content of a document), re-creating the original document based on its hash alone is out of the question. However, passwords are usually made of a limited number of characters. The very limited length of most passwords makes it possible to hash all possible combinations of letters, numbers and special characters up to a certain length with the hope of eventually guessing correctly. This would be a brute-force attack, and this is how most passwords are broken.

Hashing and Hashing

While most passwords are hashed, some are notoriously slower to recover than others. The differences are caused by several reasons.

First, not all hash functions are created equal. SHA-1 is faster than SHA-256, which is faster than SHA-512, which is still faster than Whirlpool. Depending on the choice of a hash function, the attack may run faster or slower. This can be illustrated with the following screen shot showing the time (in milliseconds) required to verify a single password protected with 500,000 rounds of certain hash functions.

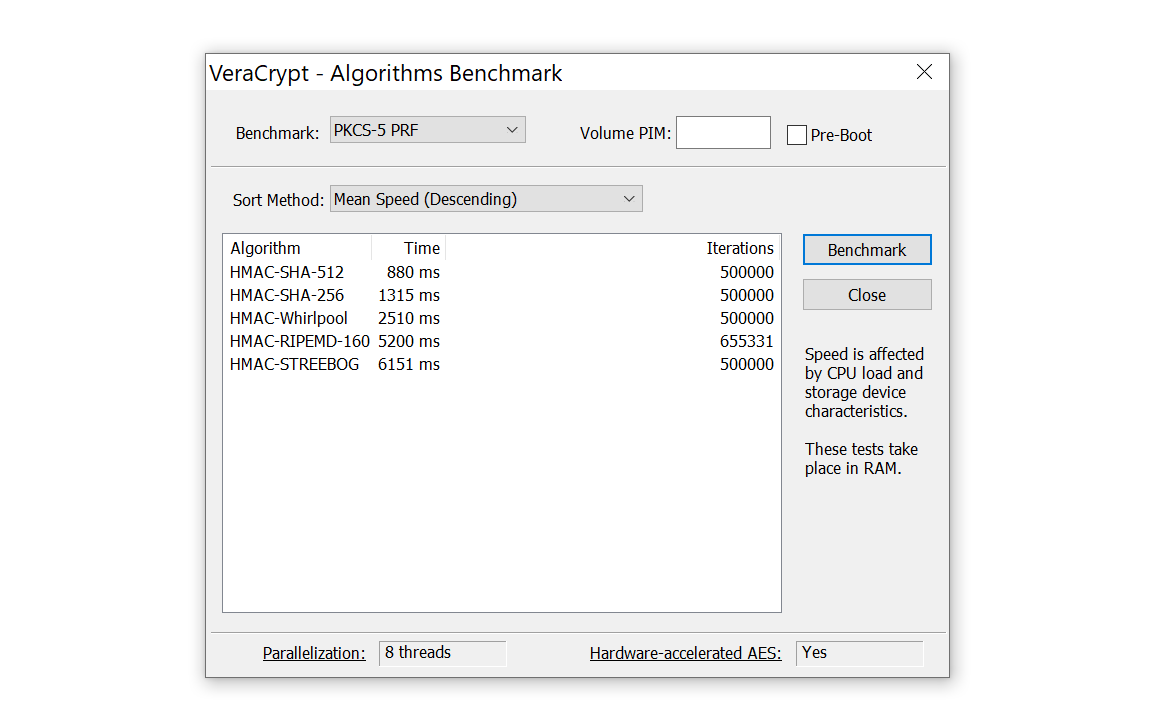
The choice of a hash function determines the password’s strength. Standard hash functions (SHA-256, SHA-512) are more than good enough.

The number of rounds (or the number of hash iterations) greatly affects the speed of verifying the password. Calculating a single hash value of a short string that is the password takes split milliseconds on modern hardware. If resources would be protected with a single hash iteration, we’d be getting attacks working at speeds in the range of tens of millions passwords per second. This is not a purely theoretical exercise; single-iteration attacks were possible in iOS 10.0 at around 6 million passwords per second on a five year old midrange Intel CPU. The more recent development enabled ultra-fast attacks on Tally Vault passwords with some 11 million passwords per second on a single i7 CPU.

Putting things into perspective, modern versions of Microsoft Office employ some 100,000 iterations for protecting documents and workbooks; a CPU-only attack produces the speed of about 10 passwords per second. Apple had bumped the number of hash iterations in iOS backups (since iOS 10.2) to 1,000,000; CPU-only attacks can now only try a handful of passwords per minute. VeraCrypt, a disk encryption tool, uses 500,000 iterations by default.

Increasing the number of hash iterations strengthens the password and slows down brute force attacks.

Hashing and Salting

There is one more thing about hashing passwords that comes to mind. What if someone wanted to take a shortcut, calculating a massive number of hashes corresponding to some 10 million most common passwords? Wouldn’t it be easier to simply look up the hash string in such a list? Or how about stealing a list of hashes and looking for some of the most common passwords in that list by their hash values? To mitigate these threats, we salt our hashes by adding unique random data to each password before calculating its hash value. The end result of this transformation is a salted password hash. To verify a salted hash, one needs the password itself and the salt value. The salt is usually stored along with the hash. Salt values stored in a separate database (or on a separate physical server) are called “pepper”.

In most circumstances, salt is absolutely required to secure your password.

All major manufacturers use salt when encrypting stuff or protecting online accounts. Exceptions are rare, but still occur.