We hear the “how long will it take to break…” question all the time. The answer is always the same: “it depends”. In this article we’ll try to give a detailed explanation and a definite answer for as many possible combinations as possible.
Do you need that password?
First thing first: are you sure you absolutely need o know that password? In many cases, protection can be removed without cracking the original password. This, for example, applies to legacy Quicken and QuickBooks documents, Microsoft Office documents saved in Microsoft Office 97-2000 or newer versions of Office in the Office 97-2003 format with default encryption settings, Microsoft SQL Server databases and certain types of Windows passwords (with few exceptions).
When instant reset is available, you might be tempted to just go this route. However, this is not always the right thing to do. As an example, resetting a Windows account password (as opposed to properly changing it from within the account itself) renders EFS (encrypted NTFS) files inaccessible. In order to decrypt those, you will need to attack and recover the original password.
One notorious case for not needing the password is 40-bit encryption. With 40-bit encryption, one can simply use a Rainbow Tables or Thunder Tables® attack on the password hash to derive the correct decryption key. With ElcomSoft tools and Thunder Tables® the process only takes seconds for 40-bit Adobe PDF encryption and 40-bit Microsoft Office 97-2000 encryption.
Passwords that can be removed instantly or near instantly include:
- Adobe PDF passwords (40-bit encryption) with Advanced PDF Password Recovery
- Microsoft Office 97-2000 documents with Advanced Office Password Breaker
- Documents saved in modern versions of Microsoft Office in Office 97-2003 Compatible mode with default encryption
- User account passwords (mind EFS and BitLocker encryption, those are not recovered)
Instant recovery or extraction
Many types of passwords can be either extracted from wherever they are stored, intercepted via the ‘man in the middle’ attack, or recovered in a matter of minutes regardless of their complexity. For example, all major Web browsers offer their own cached password storages. Google Chrome, Apple Safari, Microsoft Edge and Internet Explorer, Opera, Firefox and other Web browsers can store passwords and autocomplete forms. These passwords are loosely protected and can be extracted in a blink of an eye. POP3 and IMAP clients are another example of tools that store original passwords. In Windows, one can access many types of stored passwords such as RAS, VPN, Wi-Fi and so on.
Passwords protecting POP3 and IMAP email accounts in any desktop or mobile email client can be intercepted by emulating a Web server with Elcomsoft Advanced Mailbox Password Recovery. By authenticating to the emulated mail server, the clients will use plain-text passwords to mail accounts.
Note: this authentication method is no longer used for Exchange accounts, Outlook.com/Hotmail.com/Live.com and Gmail; those services use authentication tokens instead.
If you have to break the password
Most passwords protecting encrypted volumes, archives, mobile backups, Microsoft Office documents and other types of data are secure and must be attacked in order to be recovered. In this context, ‘attacking’ the password would mean trying various password combinations in order to find one that fits. There are different types of attacks. For example, the brute force attack would simply try all possible password combinations starting with “0” and followed with “1”, “2”, …, all the way to “ZZZZZZZZZ” or whatever the last character or special symbol there is instead of the “Z” in the chosen character set.
Since brute force is extremely inefficient for longer passwords, other types of attacks were invented to reduce the number of passwords to try. Dictionary attacks try using words from the dictionary of English language (and/or the user’s native language) as possible passwords. This would commonly include phrases and mild mutations, such as “Password1979” or “LisaPassword1”.
Dictionaries can be built from passwords extracted from other sources (e.g. from Web browsers). ElcomSoft offers a number of tools allowing to extract available passwords from the user’s computer and automatically build a custom dictionary.
So, technically speaking, there are several things affecting how fast you can break the password:
- The number of passwords to try
- Recovery speed measured in the number of passwords we can try per second
Password length and smart attacks
The number of passwords to try depends both on the length and complexity of the password itself as well as on the type(s) of attack we choose to break a given password.
Let’s clear password complexity first. Let’s look at the following charts:
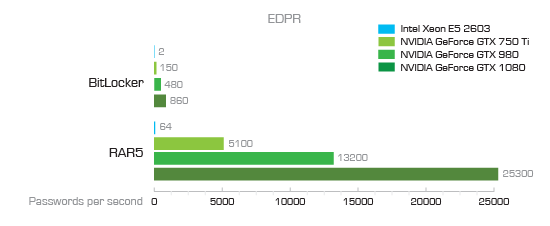
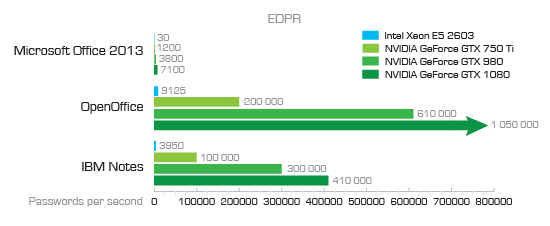
You can see that password recovery speeds vary greatly depending on the data format (more on that later). For Microsoft Office 2013 documents, we can realistically try about 7000 passwords per second if we use a single GPU acceleration unit. What does that mean, exactly? It depends on how many passwords you are about to try.
Using an online password calculator, we can calculate the exact number of possible combinations for passwords of different length and complexity. A simple password that consists of 6 lower-case letters and no numbers already has 309 million possible combinations. With a computer equipped with a GTX 1080 board that is capable of trying 7100 passwords per second (Microsoft Office 2013) you’re looking at 12 hours of straight brute-forcing. Bump the password to 8 characters, add upper-case letters and include numbers, and you’ll have 2.8 trillion possible combinations. This takes 12.5 years to break.
In other words, you’re looking at the following real-world recovery speeds:
|
Per second |
Per hour |
Per day |
| MS Office 2013 |
7100 |
25,560,000 |
613,440,000 |
| What can be broken |
2-3 characters |
4 alphanumeric characters |
5 alphanumeric characters (just barely) |
As you see, “how long will it take?” depends greatly on the password itself.
Of course, you can limit the scope of the recovery by either using a custom dictionary consisting of user’s real passwords, or employing a readily available dictionary that consists of 10,000 most popular passwords from the recent leaks. This gives you a certain chance to break even the most complex password in a matter of minutes. We already discussed these two methods in detail, please read about them here:
Factors affecting attack speeds: password length, complexity, data format and hardware
We already posted these graphs, but let’s have another look:


As you can see, the speed of attack (the number of passwords a given computer can try per second) depends on two major factors: the encryption algorithm of the protected data format, and the speed and architecture of the computer performing the attack.
The third major factor affecting the speed of the attack would be the password recovery tool itself, its optimization level as well as the ability to make use of available computational resources. We’re using Elcomsoft Distributed Password Recovery, one of the most advanced tools on the market, so at least this factor is not at play.
Depending on the data format, attack speeds may widely differ even when running on the same hardware. And even within a certain data format, the numbers may change depending on the particular implementation of the algorithm. Let’s take one example:
- iOS 9 (CPU): 2,400 passwords per second (Intel i5)
- iOS 9 (GPU): 150,000 passwords per second (NVIDIA GTX 1080)
- iOS 10.0 (CPU): 6,000,000 passwords per second (Intel i5)
- iOS 10.2 (CPU): 0.05 passwords per second (or 5-6 per minute) (Intel i5)
Back in 2016, we discovered a bug in iOS 10. Apple screwed security of iTunes backups, allowing us to try some six million passwords per second using a single CPU unit. After we published a report, Apple has quickly fixed the problem. In iOS 10.2, they went overboard and made password recovery speed extremely slow with only 5-6 passwords per minute when using a CPU, or just a few passwords per second when using a GPU. This effectively rules our brute-force attacks, only allowing for highly targeted dictionary attacks.
Another example. Microsoft appears to tighten security with every major release of Microsoft Office. While files saved by Office 97-2000 applications could be recovered near instantly, Office 2010 was already much more secure:
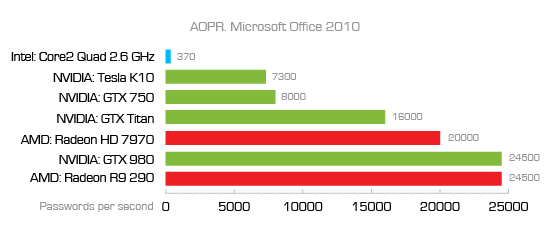
Office 2013 documents become significantly slower to break with only 30 passwords per second using a CPU or about 7100 passwords per second using a GPU. Office 2016 is slower yet. Compare that to over 1 million passwords per second for OpenOffice documents (via GPU), and you’ll begin understanding how much of a difference the data format can make.
What do these numbers mean in real terms? Let’s look at the following table.
|
6 characters, lower-case |
6 alphanumeric, both cases |
7 characters, lower case |
7 alphanumeric, both cases |
8 characters, lower case |
8 alphanumeric, both cases |
| MS Office 2013, CPU |
119 days |
60 years |
8.5 years |
3700 years |
220 years |
Eternity |
| MS Office 2013, GPU |
0,5 days |
3 months |
2 weeks |
16 years |
1 year |
975 years |
| RAR5, CPU |
56 days |
28 years |
4 years |
1744 years |
103 years |
Eternity |
| RAR5, GPU |
2 hours |
26 days |
4 days |
4.4 years |
3 months |
273 years |
| BitLocker, CPU |
5 years |
900 years |
127 years |
eternity |
3300 years |
Eternity |
| BitLocker, GPU |
4 days |
2 years |
3.6 months |
130 years |
7.7 years |
Eternity |
You can see that, for example, breaking a Microsoft Office 2013 document with a CPU alone via plain brute force can help you find a 6-character passwords consisting of lower-case letters only in 119 days (on a CPU) or in about 10 hours (if you use a single video card with a powerful GPU for hardware acceleration).
Should the user employ a significantly more complex password such as one consisting of 8 mixed letters (in both cases) and numbers, you’re looking at spending some 975 years brute-forcing that password with a single GPU.
If you have better plans for the next millennium, you can build a powerful cluster to speed up the attack. For example, you can equip each computer with 4 high-end video cards, which will cut the time from 975 years to “only” 243 years. From there, you can start adding computers to your cluster. Use a cluster of 500 computers, and you’re looking at 6-month timeframe for breaking that password. Whether it’s worth it or not is another story.
What if the user has at least one special character (such as #, $ or %) in their password? The use of special characters increases the time required to break the password by the factor of 33, meaning that the password you thought would only take a day to recover will suddenly require a full month of crunching.
You can play with the number of possible combinations by using the following password calculator:
http://projects.lambry.com/elpassword/
As an example, let’s take the simplest password that only consists of one character.
- Numbers only: 10 possible combinations
- Small letters only: 26 combinations
- Numbers and small letters: 36 combinations
- Numbers, small and capital letters: 62 combinations
- Numbers, letters in both cases, and special characters: 95 combinations
Calculating the number of passwords consisting of those character sets is as easy as raising the number of (possible combinations) to a power of (password length).
For example, a numerical password consisting of two digits has 10^2, or 100 possible combinations.
A 6-character password that consists of small letters only will have 26^6, or
308,915,776 combinations, and so on.
Dictionary attacks and mutations
If building a cluster of 500 computers is not an option, you can attempt to break long, complex passwords using a dictionary attack. During the course of a dictionary attack, the password recovery tool will not try all possible combinations of allowable characters, and will obviously miss many truly random passwords such as “A#sl73>Zds39r”. Instead, the dictionary attack attempts to combine words from a given list. The words will be combined with other words (phrases), and also combined with additional letters, symbols or modifications (mutations). For example, one of the most common mutation is making one or two characters uppercase and appending a number (sometimes, a year) to the end of the password. For example, the following passwords would all be cracked with a properly configured dictionary attack in a matter of minutes:
MyPassword1
NewPassword2017
ChangedPassword12
What is a “properly configured” dictionary attack? While there are countless numbers of possible variations (or mutations) the user can employ to make their passwords more complex to break, some of those are more common than others. The more common mutations include:
- Year, medium strength. This means that a sequence of digits representing year (e.g. 1968) will be inserted to the end of the password or between words comprising a passphrase.
- Case, medium strength. This means we’ll attempt to capitalize words using up to 2 capital letters per word.
- Digit, medium strength. This means we’ll try using digits (0-99) at the end of the password and between words comprising a passphrase.
Set up attack pipeline
In general, we recommend setting up the following attack pipeline.
- Use Top 10,000 password list (direct link) and set up a straight dictionary attack as shown here:

- In the meanwhile, use Elcomsoft Internet Password Breaker to extract user’s passwords from their computer and build a custom dictionary containing those passwords. Run an attack using this password as shown here:

- Using the same dictionary as in (2), add mild mutations and re-run the attack:
- Still using the same dictionary, add stronger mutations and re-run the attack:
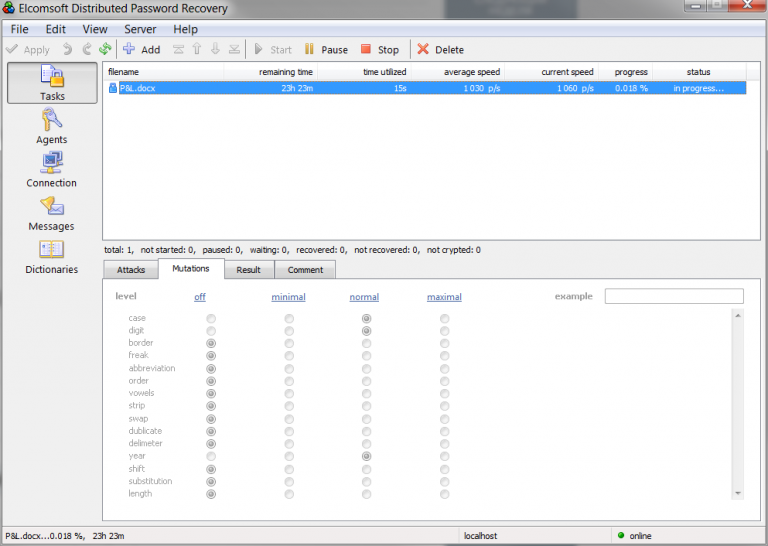
- If none of that worked, make use of the dictionary of English language possibly combined with the dictionary of the user’s native language. Configure attack using medium mutations as shown below:

- If none of that worked, estimate your chances with a brute-force attack. You may still use masks and rules to throw out some very random passwords.
Conclusion
Now you know about the different types of passwords, the time required to break them, and how to set up an attack that gives you the best chance of breaking the password in reasonable time.








